Welcome

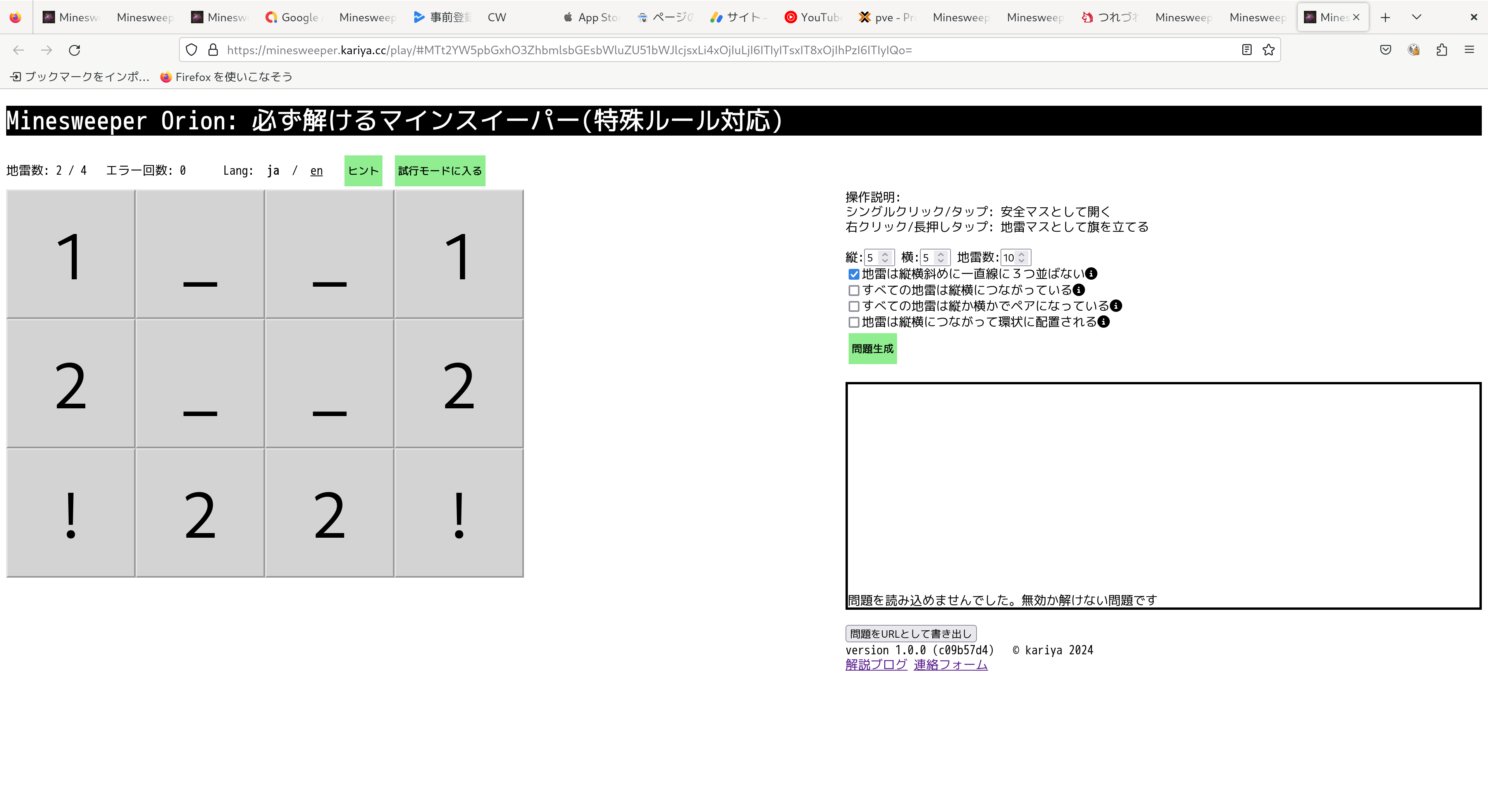
自作マインスイーパーのサイトです

とにかくプレイする

https://minesweeper.kariya.cc/play/

ゲームの解説

遊び方

ルールの解説

ゲームの特色

理詰めで必ず解けます

運要素がなく論理的に最後まで解くことができます

初期配置は毎回ランダムに生成されます

毎回違ったゲームをプレイすることができます
生成したゲームをURLとして書き出すことができます

特殊ルールを使うことができます

「地雷が縦横斜めに３個一直線に並ぶことがない」などの特殊ルールに対応しています

ブラウザーだけで遊べます

PC、スマホ、タブレットに対応しています。windows / Mac / Linux / iOS / androidなどOSは問いません

技術記事

技術記事まとめ

整数和のSATでのエンコード

SATは命題論理式をCNFという標準形で受け取ります(変数かその否定の論理和を論理積でつなげたもの)

使用しているSATライブラリーのminisatではこれを次のように表現します：

1
2
3
4
5
[
    [1, -2, 3],
    [2, 4],
    ...
]

では のような制約をどう表現すればいいでしょうか？
(この変数の和は論理和ではなくtrueなら、falseならとみなしての和を表します)
高機能なソルバーでは標準搭載されていると思いますが、今回使用したライブラリーは低水準のインターフェースしか提供していないようなので自前で実装する必要がありました

これは論理回路をSATで表現して加算器を定義することで実現できます
今回は半加算器(half adder)で用が足りたのでそれのみ示します
の結果を とし繰り上がりを (carry) とすると


が成り立りち(XOR)は論理和・積・否定で表せるので標準形に変換することができます

1
2
3
4
5
6
7
8
9
10
11
12
// x = y + z carry c
export const halfAdder = (c: Var, x: Var, y: Var, z: Var): Cnf => {
  return [
    [-c, y],
    [-c, z],
    [c, -y, -z],
    [-x, -y, -z],
    [-x, y, z],
    [x, -y, z],
    [x, y, -z],
  ];
};

（なおCNFはWolframAlphaで計算できます
https://www.wolframalpha.com/input?i=CNF+of++%28x+equivalent+y+xor+z%29+and+%28c+equivalent+y+and+z%29&lang=ja
）

半加算器ができたので を実装します

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
export const sumEq = (xs: Var[], n: int, newVar: () => Var): Cnf => {
  if (xs.length === 0) {
    if (n === 0) return cnfTrue;
    return cnfFalse;
  }
  if (n === 0) return xs.map(x => [-x]);
  if (n === xs.length) return xs.map(x => [x]);
  if (n < 0 || n > xs.length) return cnfFalse;

  let result: Cnf= [];
  // xsの累積和の最下位ビット
  let t = xs[0];
  let cs: int[] = [];
  for (const x of xs.slice(1)) {
    const c = newVar();
    const v = newVar();
    result = result.concat(halfAdder(c, v, x, t));
    t = v;
    cs.push(c);
  }
  if (n % 2 === 0) {
    result.push([-t]); // t === 0
  } else {
    result.push([t]); // t === 1
  }
  result = result.concat(sumEq(cs, Math.floor(n / 2), newVar));
  return result;
};

同様にも実装できます

「必ず解ける」を保証する仕組み

SATソルバーを使用しています（SATの説明は別記事予定）
行列のマスが地雷かを変数で表現します。
がTrueならそのマスに地雷があることを、Falseなら地雷がないことを表します。
下記のようにルールをSATの条件として統一して扱うことができます

地雷数

総地雷数をとして盤上の全マス目についてで表します
ここではがTrueなら、Falseならとして和を取ることを表します
単純なSATでは和はそのまま表現できないので工夫が必要でした（整数和をSATでエンコード）

通常のヒント

画像の例ではを満たすがあるかを調べればよいです

特殊ルール

「縦横斜めに一直線に３個地雷が並ばない」

これは３連続のマス目をすべて列挙してその中のの和が3でないことを制約とします
上記とは異なり和が~で「ない」ことをSATで表現する必要があります

「すべての地雷が縦横につながっている」

マス目をノードとしその上下左右のマスとの間にエッジがあるグラフを考えます
地雷の総数をとしてこのグラフにサイズの連結サブグラフがあるかを制約にします
グラフの条件もSATにエンコードする必要がありました

「すべての地雷が縦横でペアになっている」

縦横２マスを総列挙してそれぞれの和がかになるという制約で表します

特殊ルールとは

通常のマインスイパーのルールに加えて次のようなルールがあります
また新ルールを開発中です

地雷が３個並ばない

縦か横、斜めに地雷が３個一直線に並ぶことがないということです

地雷が1つにつながっている

すべての地雷が縦か横につながっています（斜めはつながっているとみなしません）
孤立した地雷群がないということです

地雷がペアになっている

すべての地雷が縦か横にペアになって配置されます(1x2か2x1の形)
ペア同士がつながることはありません

ゲームの遊び方

「問題生成」ボタンを押します

少し時間がかかります。状況がメッセージ欄に表示されるので終了するまで待ちます
盤面のサイズ、地雷の数を設定することができます。大きくしすぎると生成が終わらないので少しずつ調整してください

操作方法

左クリック(タブレットなどはタッチ)で安全マスとして開きます。
右クリック(タブレットなどでは長押しタッチ)で地雷マスとして旗を置きます。
その時点の盤面の情報から確定していないマスを開くとエラーが出ます
わからない場合は「ヒント」ボタンを押すと開くことができるマスが表示されます